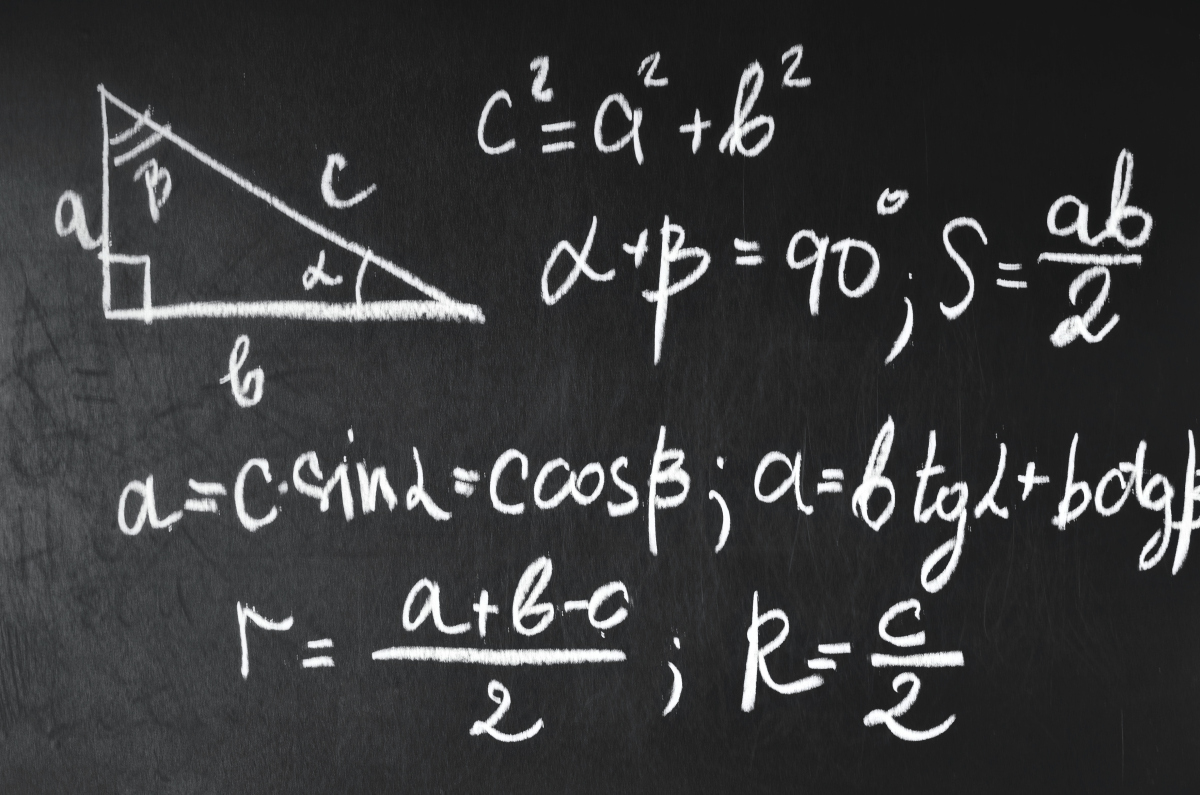
一、勾股定理的历史渊源

勾股定理最早可以追溯到公元前7世纪的中国商代时期，那时的数学家们已经发现了“勾3股4弦5”的勾股定理特例。而在古希腊时期，著名数学家毕达哥拉斯学派更是将勾股定理发扬光大，将其应用于音乐、哲学等多个领域。勾股定理的悠久历史见证了人类对数学知识的不断探索和追求。

二、勾股定理的数学原理

勾股定理是一个关于直角三角形的边长关系的定理。它表述为：在直角三角形中，直角边的平方和等于斜边的平方。用数学公式表示就是：a² + b² = c²，其中a和b是直角三角形的两条直角边，c是斜边。这个定理在数学上具有重要的地位，它是证明其他定理和公式的基础，也是解决几何问题的重要工具。

三、勾股定理的证明方法

勾股定理的证明方法多种多样，其中包括赵爽弦图证明、毕达哥拉斯证明、欧几里得证明等。这些证明方法虽然各有特色，但都是基于几何图形和代数运算的结合，通过严谨的逻辑推理来证明勾股定理的正确性。

四、勾股定理在现代生活中的应用

勾股定理不仅在数学领域具有重要地位，还在现代生活中有着广泛的应用。例如，在建筑工程中，工程师们可以利用勾股定理计算建筑物的高度和距离；在导航和地理信息系统中，勾股定理也被用来计算地球上两点之间的距离；此外，在物理学、计算机科学等领域，勾股定理也发挥着不可或缺的作用。

通过对勾股定理的深入了解，我们可以发现这个简单的数学公式背后蕴含着丰富的人类智慧和数学知识。从古代到现代，勾股定理一直在推动着数学和科学的发展，为人类文明进步做出了巨大的贡献。作为科普创作者，我们希望通过这篇文章激发大家对数学的兴趣和热爱，让我们共同探索数学世界的奥秘和美丽。

在这个数字化、信息化的时代，数学作为一门基础学科，仍然发挥着不可替代的作用。无论是在科学研究、工程技术还是日常生活中，我们都能感受到数学的力量和魅力。因此，让我们继续传承和发扬勾股定理等数学知识的智慧，为人类的未来发展贡献自己的力量。