磁量子数：揭秘原子世界中的空间取向密码

在微观粒子的奇妙世界里，电子如同一个个神秘的舞者，在原子内部的特定区域内舞动。要精准描述这些电子的运动状态，量子力学为我们提供了一套独特的 “密码体系”，而磁量子数便是这套体系中不可或缺的重要组成部分。它不像主量子数那样直接关联电子运动轨道的能量高低，也不像角量子数那样决定轨道的形状，而是专注于揭示电子轨道在空间中的具体取向，为我们理解原子的磁学性质、光谱分裂等现象打开了关键的一扇门。

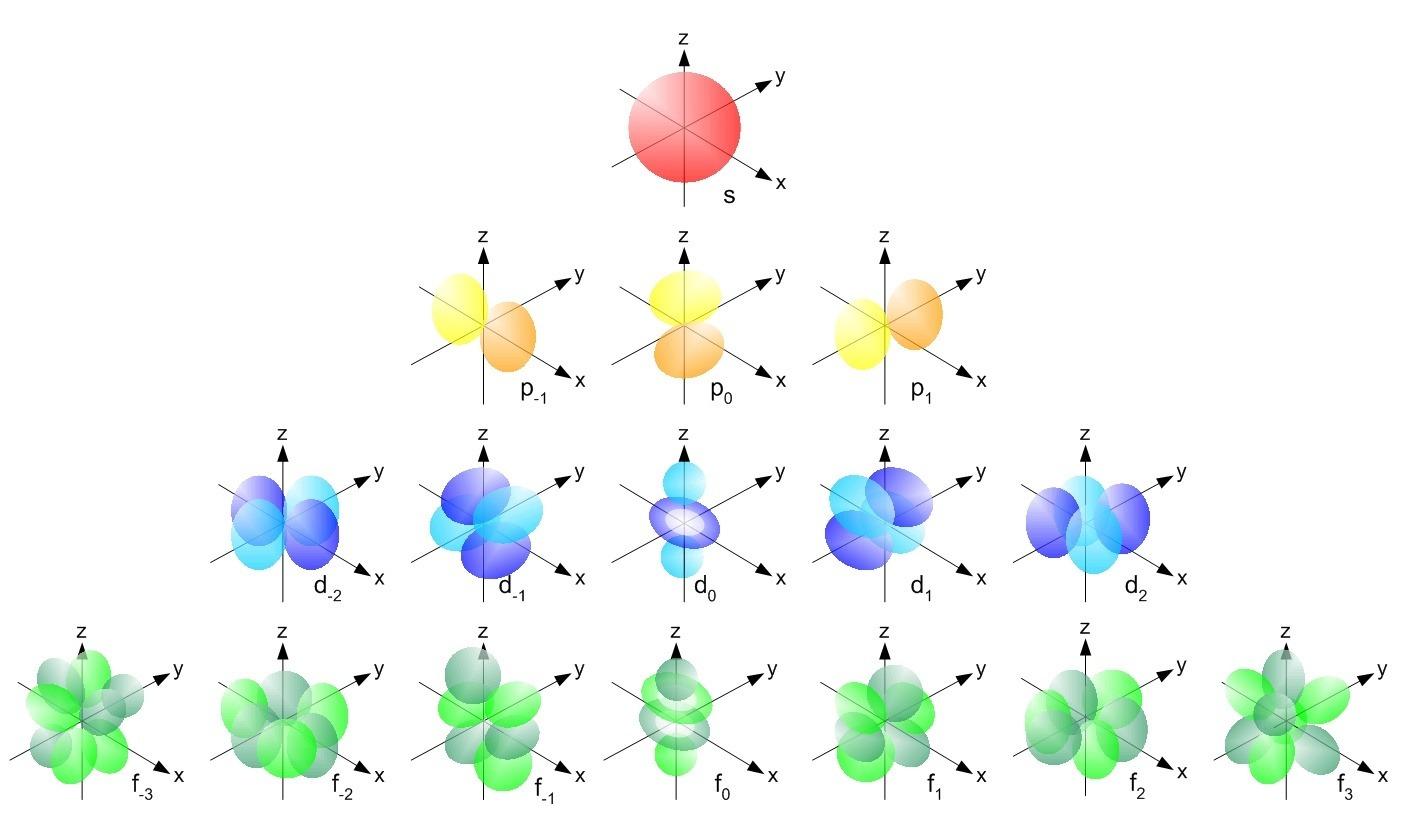
磁量子数通常用符号 “mₗ” 来表示，它的存在与角量子数 “l” 有着紧密的联系，角量子数决定了电子亚层的类型，而磁量子数则进一步细化了该亚层中电子轨道的空间分布。不同的角量子数对应着不同形状的电子轨道，比如当 l=0 时，对应的是球形的 s 轨道；l=1 时，是哑铃形的 p 轨道；l=2 时，是更为复杂的花瓣形 d 轨道等。而磁量子数的取值范围则严格依赖于角量子数的数值，其可能的取值为从 – l 到 + l 的所有整数，包括 0 在内。这就意味着，对于特定的角量子数 l，磁量子数 mₗ会有 (2l+1) 种不同的取值，每一种取值都代表着电子轨道在空间中的一种独特取向。

以常见的电子亚层为例，当 l=0（即 s 亚层）时，根据磁量子数的取值规则，mₗ只能取 0 这一个值，这表明 s 亚层只有一种空间取向的轨道，也就是我们常说的 s 轨道，其在空间中呈现出球对称的分布特征，无论从哪个方向观察，其形状和分布都保持一致，不存在方向性差异。这种球对称性使得 s 轨道上的电子在空间中的分布相对均匀，也使得 s 亚层在参与原子成键等过程中表现出独特的性质。

当 l=1（即 p 亚层）时，磁量子数 mₗ的取值范围则变为 – 1、0、+1，共 3 种不同的取值，这也就意味着 p 亚层存在 3 种空间取向不同的轨道，分别被称为 pₓ轨道、pᵧ轨道和 p_z 轨道。这三种轨道在空间中相互垂直，它们的对称轴分别沿着 x 轴、y 轴和 z 轴方向。从形状上看，每一种 p 轨道都呈现出哑铃状，由两个大小相等、方向相反的 “lobe”（瓣）组成，两个瓣的中心连线即为轨道的对称轴，而在两个瓣的中间位置，电子出现的概率为零，这个区域被称为节面。由于这三种 p 轨道在空间取向的不同，它们在与其他原子的轨道发生重叠形成化学键时，会根据成键方向的不同而表现出不同的成键能力和方式，进而影响分子的空间构型和化学性质。

对于 l=2（即 d 亚层），磁量子数 mₗ的取值则更为丰富，包括 – 2、-1、0、+1、+2，共 5 种不同的取值，对应着 d 亚层的 5 种空间取向不同的轨道，分别标记为 dₓᵧ、dₓz、dᵧz、dₓ²₋ᵧ² 和 d_z² 轨道。这些 d 轨道的形状比 s 轨道和 p 轨道更为复杂，大多呈现出花瓣形的结构，但不同 d 轨道的花瓣数量、分布方向和空间对称性存在明显差异。例如，dₓᵧ、dₓz、dᵧz 这三种轨道的形状相似，都有 4 个瓣，且这些瓣分别位于坐标轴所形成的平面内，如 dₓᵧ轨道的瓣就位于 x-y 平面内，且沿着 x 轴和 y 轴的对角线方向分布；而 dₓ²₋ᵧ² 轨道同样有 4 个瓣，但其瓣沿着 x 轴和 y 轴的正方向和负方向分布；d_z² 轨道则较为特殊，它由两个沿 z 轴方向分布的 “雪茄形” 瓣和一个围绕 z 轴的环形区域组成。d 亚层的这些轨道因其多样的空间取向和复杂的形状，在过渡金属原子中扮演着至关重要的角色，过渡金属原子的许多特殊性质，如可变的氧化态、形成配合物的能力以及独特的颜色等，都与 d 轨道上电子的排布和运动状态密切相关，而磁量子数对 d 轨道空间取向的定义，正是理解这些性质的基础。

磁量子数的重要性不仅体现在对电子轨道空间取向的描述上，更在解释原子光谱的分裂现象中发挥着关键作用。在没有外磁场存在的情况下，同一亚层中不同空间取向的轨道（即具有不同磁量子数的轨道）具有相同的能量，这些轨道被称为简并轨道。例如，p 亚层的 3 个轨道在无外磁场时能量完全相同，d 亚层的 5 个轨道也是如此。然而，当原子处于外磁场中时，这种简并状态会被打破，原本能量相同的简并轨道会分裂成能量不同的若干个轨道，这种现象被称为塞曼效应。塞曼效应的产生正是由于不同磁量子数对应的电子轨道在磁场中具有不同的能量。电子轨道可以看作是一个微小的磁偶极子，当处于外磁场中时，会与外磁场发生相互作用，而相互作用的能量大小则取决于轨道的空间取向，也就是磁量子数的数值。磁量子数不同，轨道的空间取向不同，与外磁场的相互作用强度就不同，从而导致轨道的能量发生差异，最终使得原子光谱中的某一条谱线分裂成多条谱线。通过对塞曼效应的研究，科学家们不仅验证了磁量子数的存在和取值规律，还能够深入了解原子内部电子的运动状态和原子的磁学性质，为量子力学的发展提供了有力的实验支持。

此外，磁量子数在理解原子的磁性方面也具有重要意义。原子的磁性主要来源于电子的自旋和电子轨道的运动。电子轨道运动所产生的磁矩与磁量子数密切相关，不同磁量子数对应的轨道磁矩在空间中的取向不同，其对原子总磁矩的贡献也不同。当原子中存在未成对电子时，这些电子的轨道磁矩和自旋磁矩会共同作用，使得原子表现出顺磁性；而当原子中的电子全部成对时，电子的轨道磁矩和自旋磁矩会相互抵消，原子则表现出抗磁性。通过对磁量子数的研究，我们可以更清晰地了解电子轨道磁矩的分布和变化规律，进而深入理解原子磁性的本质，为设计和开发具有特定磁性的材料提供理论指导，如永磁材料、软磁材料等，这些材料在电子设备、能源存储、医疗设备等领域都有着广泛的应用。

在原子结构的学习和研究中，磁量子数与主量子数、角量子数和自旋量子数共同构成了完整的量子数体系，它们从不同的角度描述了电子在原子中的运动状态。主量子数 n 决定了电子所处的电子层，角量子数 l 决定了电子层中的亚层和轨道形状，磁量子数 mₗ决定了亚层中轨道的空间取向，而自旋量子数 mₛ则描述了电子自身的自旋运动状态。这四个量子数相互配合、相互补充，缺一不可，共同构成了描述电子运动状态的完整 “密码”。只有掌握了这四个量子数的内涵和它们之间的关系，我们才能真正理解原子内部电子的排布规律和运动特性，进而解释原子的化学性质、物理性质以及各种微观现象。

磁量子数作为量子力学中的重要概念，其价值不仅仅在于理论层面的描述和解释，更在实际的科学研究和技术应用中发挥着重要作用。从对原子光谱的分析到对材料磁性的研究，从量子计算的探索到新型功能材料的开发，磁量子数都扮演着不可或缺的角色。它就像一把钥匙，为我们打开了通往原子微观世界的大门，让我们能够更深入地探索微观粒子的运动规律和本质特性。那么，当我们进一步结合其他量子数去研究更复杂的原子体系或分子体系时，又会发现磁量子数带来哪些新的惊喜和挑战呢？